9.5 Real Distribution Families
The distribution object constructors documented in this section return uniquely defined distributions for the largest possible parameter domain. This usually means that they return distributions for a larger domain than their mathematical counterparts are defined on.
> (pdf (normal-dist 1 0) 1) +inf.0
> (pdf (normal-dist 1 0) 1.0000001) 0.0
Some parameters’ boundary values give rise to non-unique limits. Sometimes the ambiguity can be resolved using necessary properties; see Gamma-Dist for an example. When no resolution exists, as with (beta-dist 0 0), which puts an indeterminate probability on the value 0 and the rest on 1, the constructor returns an undefined distribution.
Some distribution object constructors attempt to return sensible distributions when given special values such as +inf.0 as parameters. Do not count on these yet.
Many distribution families, such as Gamma-Dist, can be parameterized on either scale or rate (which is the reciprocal of scale). In all such cases, the implementations provided by math/distributions are parameterized on scale.
9.5.1 Beta Distributions
Wikipedia: Beta Distribution.
syntax
procedure
alpha : Real beta : Real
procedure
(beta-dist-alpha d) → Flonum
d : Beta-Dist
procedure
(beta-dist-beta d) → Flonum
d : Beta-Dist
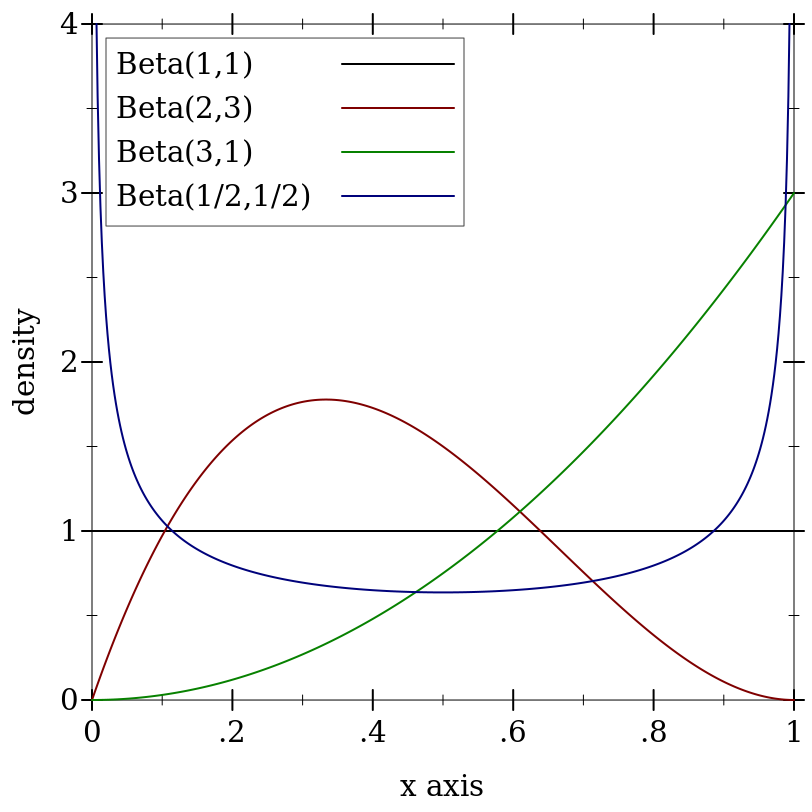
> (plot (for/list ([α (in-list '(1 2 3 1/2))] [β (in-list '(1 3 1 1/2))] [i (in-naturals)]) (function (distribution-pdf (beta-dist α β)) #:color i #:label (format "Beta(~a,~a)" α β))) #:x-min 0 #:x-max 1 #:y-max 4 #:y-label "density")
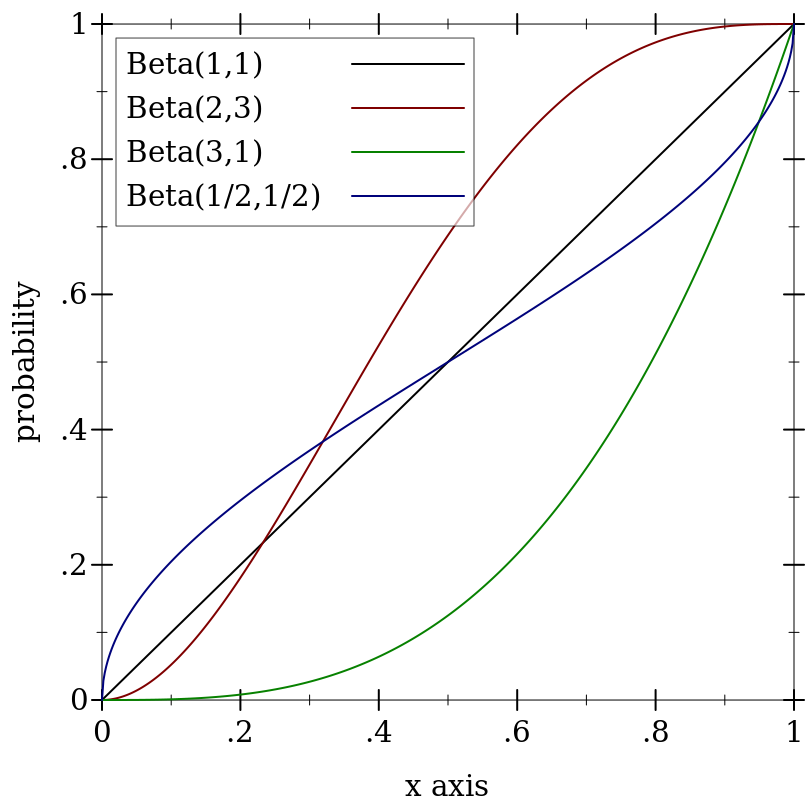
> (plot (for/list ([α (in-list '(1 2 3 1/2))] [β (in-list '(1 3 1 1/2))] [i (in-naturals)]) (function (ordered-dist-cdf (beta-dist α β)) #:color i #:label (format "Beta(~a,~a)" α β))) #:x-min 0 #:x-max 1 #:y-label "probability")
(beta-dist 0 0) and (beta-dist +inf.0 +inf.0) are undefined distributions.
When a = 0 or b = +inf.0, the returned distribution acts like (delta-dist 0).
When a = +inf.0 or b = 0, the returned distribution acts like (delta-dist 1).
9.5.2 Cauchy Distributions
Wikipedia: Cauchy Distribution.
syntax
procedure
(cauchy-dist [mode scale]) → Cauchy-Dist
mode : Real = 0 scale : Real = 1
procedure
(cauchy-dist-mode d) → Flonum
d : Cauchy-Dist
procedure
(cauchy-dist-scale d) → Flonum
d : Cauchy-Dist
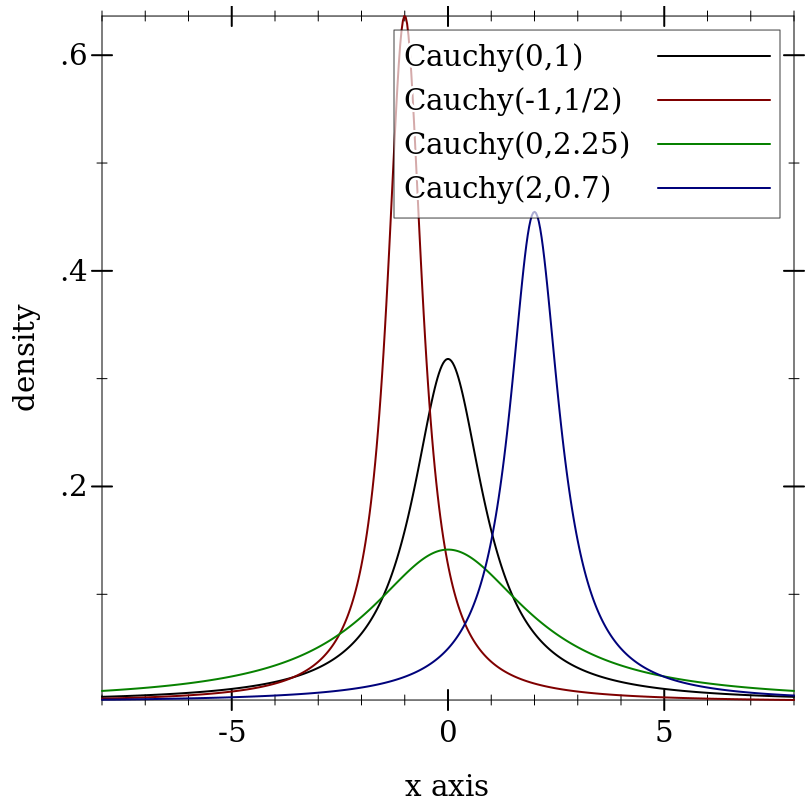
> (plot (for/list ([m (in-list '(0 -1 0 2))] [s (in-list '(1 1/2 2.25 0.7))] [i (in-naturals)]) (function (distribution-pdf (cauchy-dist m s)) #:color i #:label (format "Cauchy(~a,~a)" m s))) #:x-min -8 #:x-max 8 #:y-label "density" #:legend-anchor 'top-right)
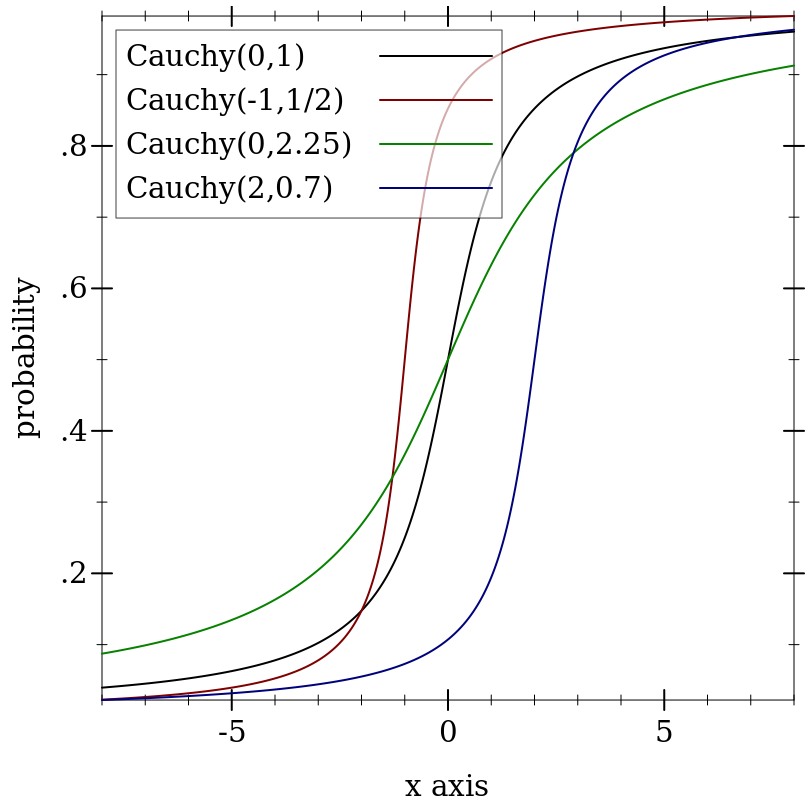
> (plot (for/list ([m (in-list '(0 -1 0 2))] [s (in-list '(1 1/2 2.25 0.7))] [i (in-naturals)]) (function (ordered-dist-cdf (cauchy-dist m s)) #:color i #:label (format "Cauchy(~a,~a)" m s))) #:x-min -8 #:x-max 8 #:y-label "probability")
9.5.3 Delta Distributions
Wikipedia: Dirac Delta Function.
syntax
procedure
(delta-dist [mean]) → Delta-Dist
mean : Real = 0
procedure
(delta-dist-mean d) → Flonum
d : Delta-Dist
> (pdf (delta-dist) 0) +inf.0
> (pdf (delta-dist) 1) 0.0
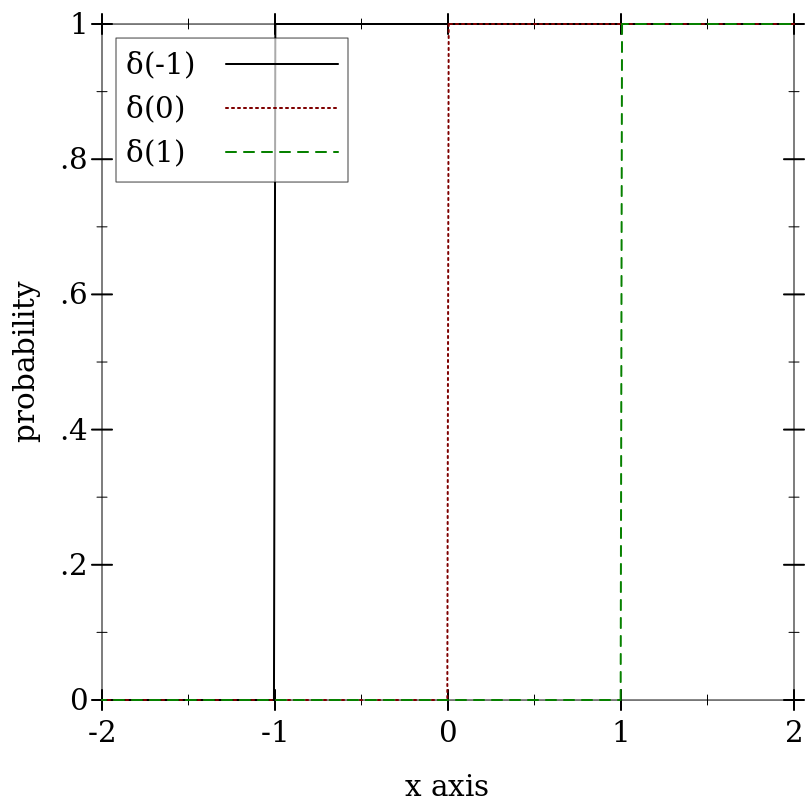
> (plot (for/list ([μ (in-list '(-1 0 1))] [i (in-naturals)]) (function (ordered-dist-cdf (delta-dist μ)) #:color i #:style i #:label (format "δ(~a)" μ))) #:x-min -2 #:x-max 2 #:y-label "probability")
9.5.4 Exponential Distributions
Wikipedia: Exponential Distribution.
syntax
procedure
(exponential-dist [mean]) → Exponential-Dist
mean : Real = 1
procedure
(exponential-dist-mean d) → Flonum
d : Exponential-Dist
(exponential-dist (/ 1.0 rate))
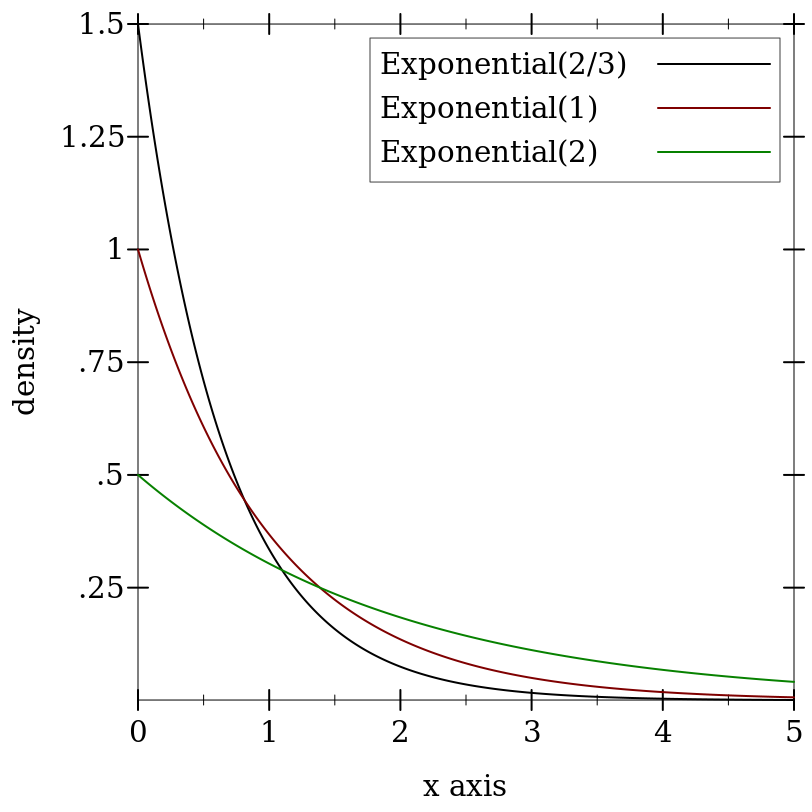
> (plot (for/list ([μ (in-list '(2/3 1 2))] [i (in-naturals)]) (function (distribution-pdf (exponential-dist μ)) #:color i #:label (format "Exponential(~a)" μ))) #:x-min 0 #:x-max 5 #:y-label "density" #:legend-anchor 'top-right)
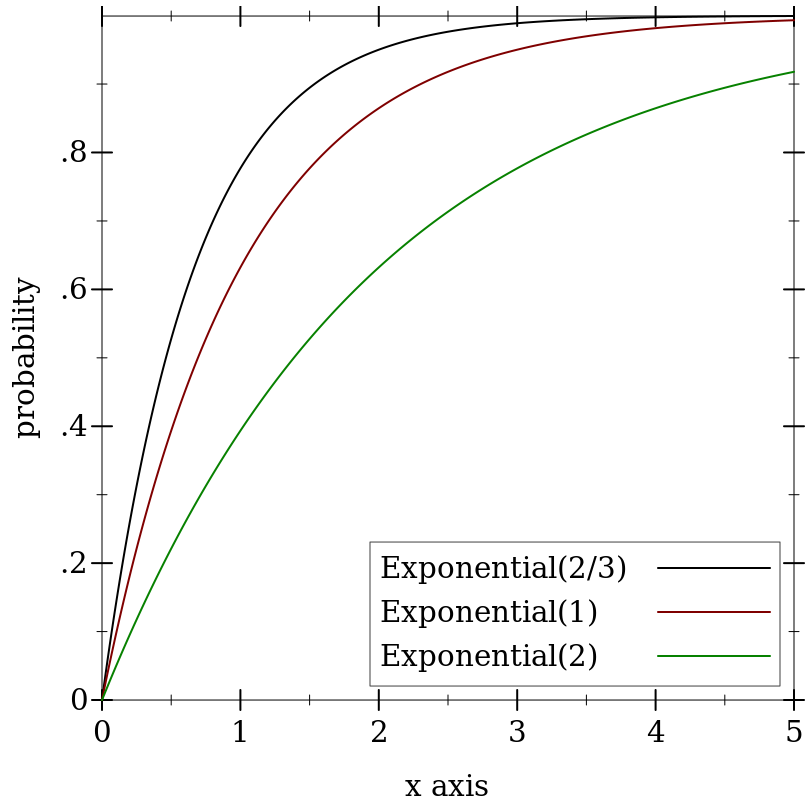
> (plot (for/list ([μ (in-list '(2/3 1 2))] [i (in-naturals)]) (function (ordered-dist-cdf (exponential-dist μ)) #:color i #:label (format "Exponential(~a)" μ))) #:x-min 0 #:x-max 5 #:y-label "probability" #:legend-anchor 'bottom-right)
9.5.5 Gamma Distributions
Wikipedia: Gamma Distribution.
syntax
procedure
(gamma-dist [shape scale]) → Gamma-Dist
shape : Real = 1 scale : Real = 1
procedure
(gamma-dist-shape d) → Flonum
d : Gamma-Dist
procedure
(gamma-dist-scale d) → Flonum
d : Gamma-Dist
(gamma-dist shape (/ 1.0 rate))
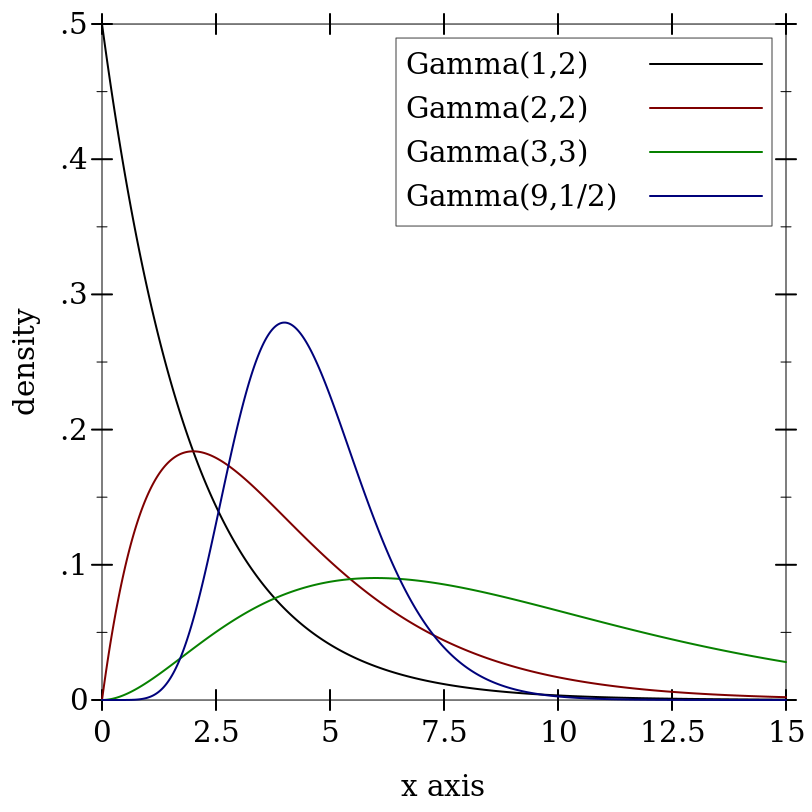
> (plot (for/list ([k (in-list '(1 2 3 9))] [s (in-list '(2 2 3 1/2))] [i (in-naturals)]) (function (distribution-pdf (gamma-dist k s)) #:color i #:label (format "Gamma(~a,~a)" k s))) #:x-min 0 #:x-max 15 #:y-label "density" #:legend-anchor 'top-right)
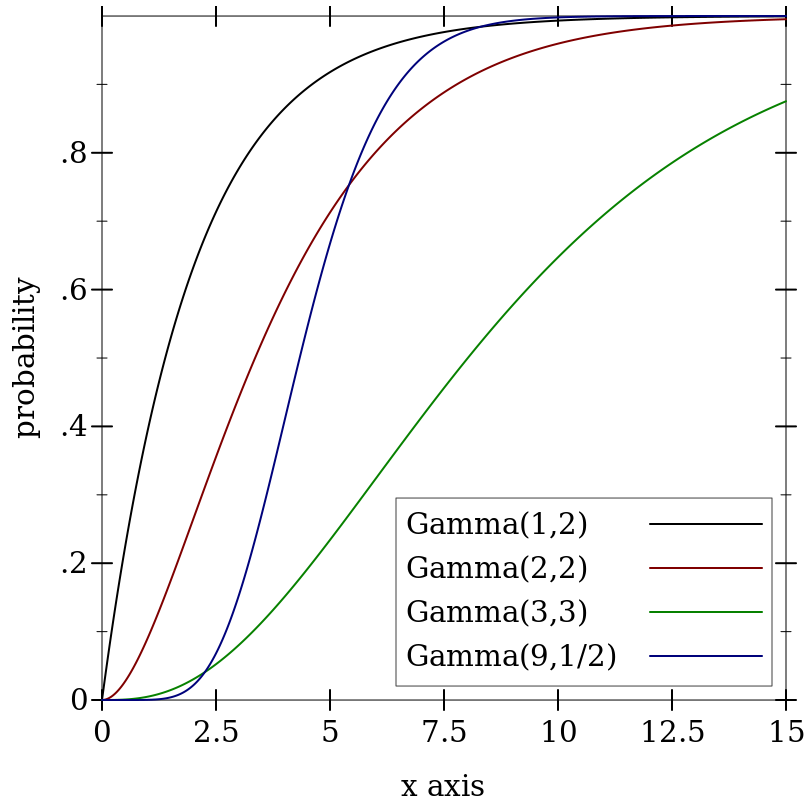
> (plot (for/list ([k (in-list '(1 2 3 9))] [s (in-list '(2 2 3 1/2))] [i (in-naturals)]) (function (ordered-dist-cdf (gamma-dist k s)) #:color i #:label (format "Gamma(~a,~a)" k s))) #:x-min 0 #:x-max 15 #:y-label "probability" #:legend-anchor 'bottom-right)
> (cdf (gamma-dist 0 1) 0) 1.0
9.5.6 Weibull Distributions
Wikipedia: Weibull Distribution.
syntax
procedure
(weibull-dist shape [location scale]) → Weibull-Dist
shape : Positive-Real location : Real = 0 scale : Real = 1
procedure
k : Weibull-Dist
procedure
(weibull-dist-location d) → Real
d : Weibull-Dist
procedure
(weibull-dist-scale d) → Real
d : Weibull-Dist
> (plot (for/list ([k (in-list '(1/2 1 1 5))] [d (in-list '(0 0 3/2 0))] [s (in-list '(1 1 2 1))] [i (in-naturals)]) (function (distribution-pdf (weibull-dist k d s)) #:color i #:label (if (and (= d 0) (= s 1)) (format "Weibull(~a)" k) (format "Weibull(~a,~a,~a)" k d s)))) #:x-min 0 #:x-max 6 #:y-label "density" #:legend-anchor 'top-right)
> (plot (for/list ([k (in-list '(1/2 1 1 5))] [d (in-list '(0 0 3/2 0))] [s (in-list '(1 1 2 1))] [i (in-naturals)]) (function (ordered-dist-cdf (weibull-dist k d s)) #:color i #:label (if (and (= d 0) (= s 1)) (format "Weibull(~a)" k) (format "Weibull(~a,~a,~a)" k d s)))) #:x-min 0 #:x-max 10 #:y-label "probability" #:legend-anchor 'bottom-right)
9.5.7 Logistic Distributions
Wikipedia: Logistic Distribution.
syntax
procedure
(logistic-dist [mean scale]) → Logistic-Dist
mean : Real = 0 scale : Real = 1
procedure
(logistic-dist-mean d) → Flonum
d : Logistic-Dist
procedure
(logistic-dist-scale d) → Flonum
d : Logistic-Dist
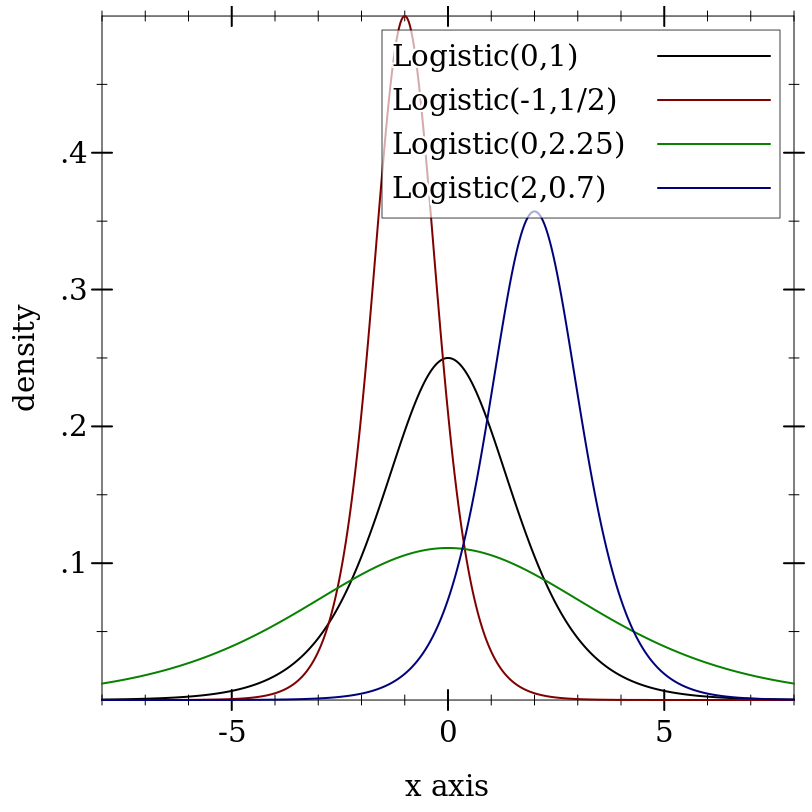
> (plot (for/list ([μ (in-list '(0 -1 0 2))] [s (in-list '(1 1/2 2.25 0.7))] [i (in-naturals)]) (function (distribution-pdf (logistic-dist μ s)) #:color i #:label (format "Logistic(~a,~a)" μ s))) #:x-min -8 #:x-max 8 #:y-label "density" #:legend-anchor 'top-right)
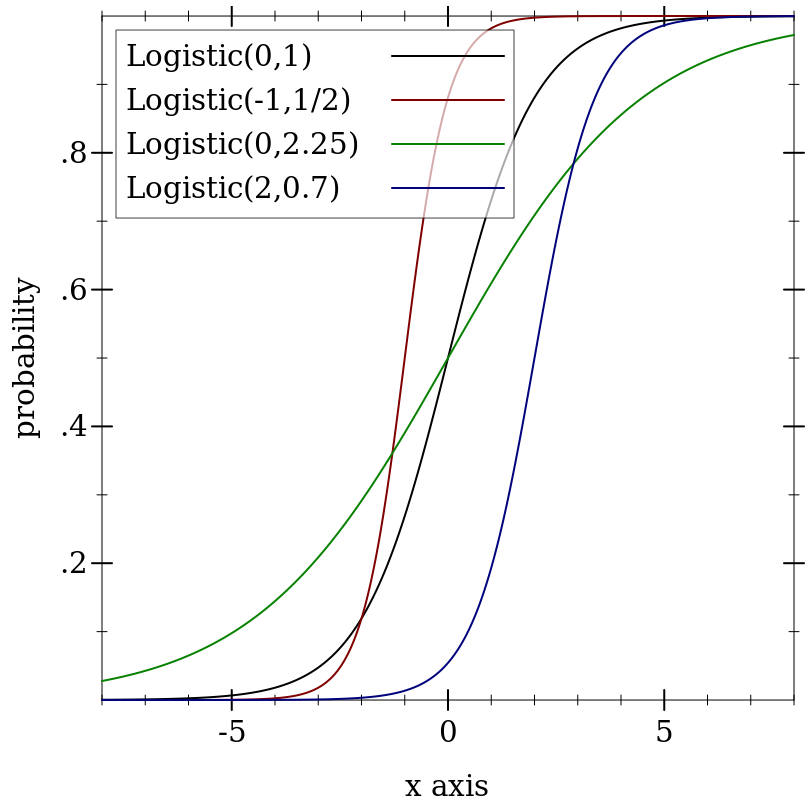
> (plot (for/list ([μ (in-list '(0 -1 0 2))] [s (in-list '(1 1/2 2.25 0.7))] [i (in-naturals)]) (function (ordered-dist-cdf (logistic-dist μ s)) #:color i #:label (format "Logistic(~a,~a)" μ s))) #:x-min -8 #:x-max 8 #:y-label "probability")
9.5.8 Normal Distributions
Wikipedia: Normal Distribution.
syntax
procedure
(normal-dist [mean stddev]) → Normal-Dist
mean : Real = 0 stddev : Real = 1
procedure
(normal-dist-mean d) → Flonum
d : Normal-Dist
procedure
(normal-dist-stddev d) → Flonum
d : Normal-Dist
(normal-dist mean (sqrt var))
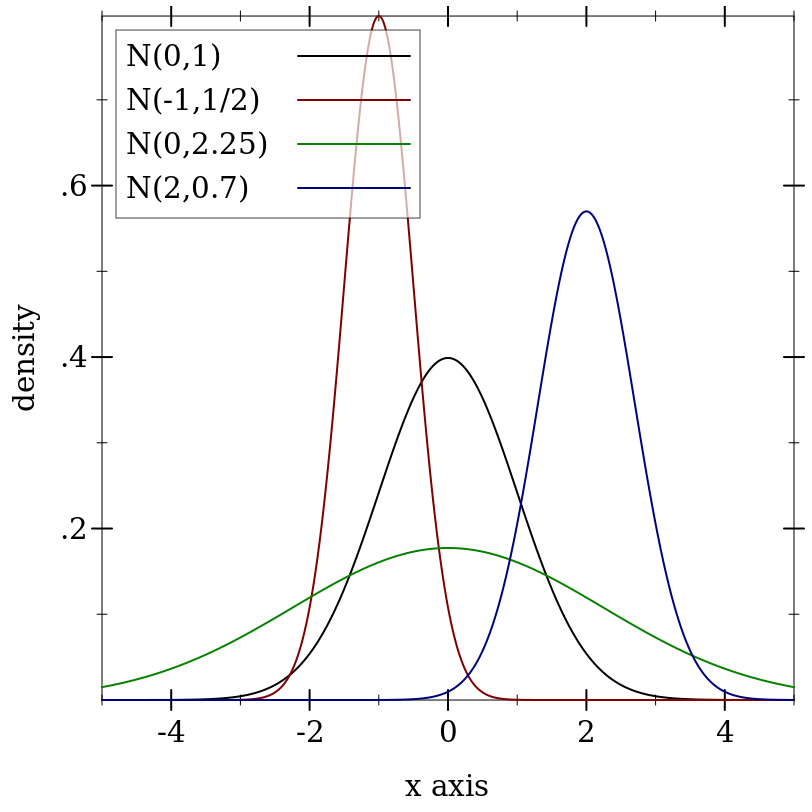
> (plot (for/list ([μ (in-list '(0 -1 0 2))] [σ (in-list '(1 1/2 2.25 0.7))] [i (in-naturals)]) (function (distribution-pdf (normal-dist μ σ)) #:color i #:label (format "N(~a,~a)" μ σ))) #:x-min -5 #:x-max 5 #:y-label "density")
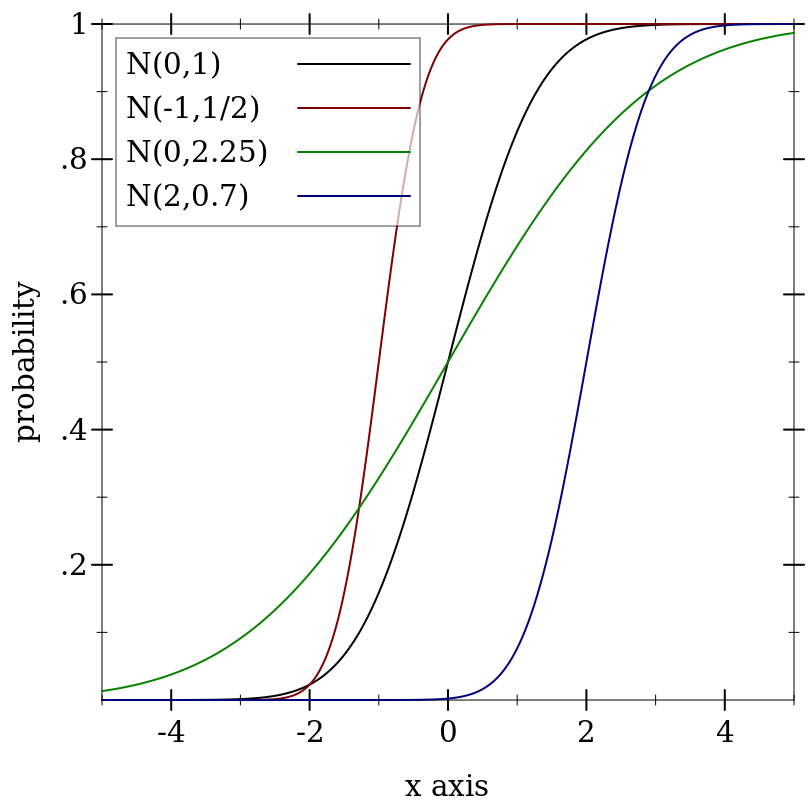
> (plot (for/list ([μ (in-list '(0 -1 0 2))] [σ (in-list '(1 1/2 2.25 0.7))] [i (in-naturals)]) (function (ordered-dist-cdf (normal-dist μ σ)) #:color i #:label (format "N(~a,~a)" μ σ))) #:x-min -5 #:x-max 5 #:y-label "probability")
9.5.9 Student-t Distributions
Wikipedia: Student-t Distribution.
syntax
procedure
(student-t-dist freedom [mean scale]) → Student-t-Dist
freedom : Positive-Real mean : Real = 0 scale : Real = 1
procedure
d : Student-t-Dist
procedure
(student-t-dist-mean d) → Real
d : Student-t-Dist
procedure
(student-t-dist-scale d) → Real
d : Student-t-Dist
> (plot (for/list ([ν (in-list '(1 2 3 5.5))] [μ (in-list '(0 0 0 2.3))] [σ (in-list '(1 1 1 0.4))] [i (in-naturals)]) (function (distribution-pdf (student-t-dist ν μ σ)) #:color i #:label (if (and (= μ 0) (= σ 1)) (format "Stud-t(~a)" ν) (format "Stud-t(~a,~a,~a)" ν μ σ)))) #:x-min -5 #:x-max 10 #:y-label "density")
> (plot (for/list ([ν (in-list '(1 2 3 5.5))] [μ (in-list '(0 0 0 2.3))] [σ (in-list '(1 1 1 0.4))] [i (in-naturals)]) (function (ordered-dist-cdf (student-t-dist ν μ σ)) #:color i #:label (if (and (= μ 0) (= σ 1)) (format "Stud-t(~a)" ν) (format "Stud-t(~a,~a,~a)" ν μ σ)))) #:x-min -5 #:x-max 10 #:y-label "probability")
9.5.10 Triangular Distributions
Wikipedia: Triangular Distribution.
syntax
procedure
(triangle-dist [min max mode]) → Triangle-Dist
min : Real = 0 max : Real = 1 mode : Real = (* 0.5 (+ min max))
procedure
(triangle-dist-min d) → Flonum
d : Triangle-Dist
procedure
(triangle-dist-max d) → Flonum
d : Triangle-Dist
procedure
(triangle-dist-mode d) → Flonum
d : Triangle-Dist
If min, mode and max are not in ascending order, they are sorted before constructing the distribution object.
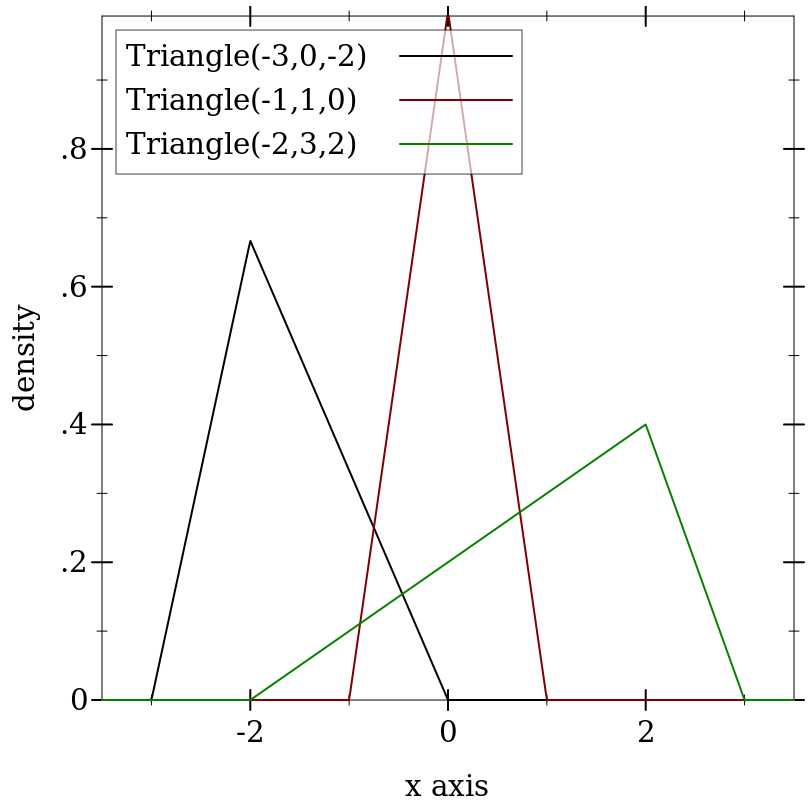
> (plot (for/list ([a (in-list '(-3 -1 -2))] [b (in-list '(0 1 3))] [m (in-list '(-2 0 2))] [i (in-naturals)]) (function (distribution-pdf (triangle-dist a b m)) #:color i #:label (format "Triangle(~a,~a,~a)" a b m))) #:x-min -3.5 #:x-max 3.5 #:y-label "density")
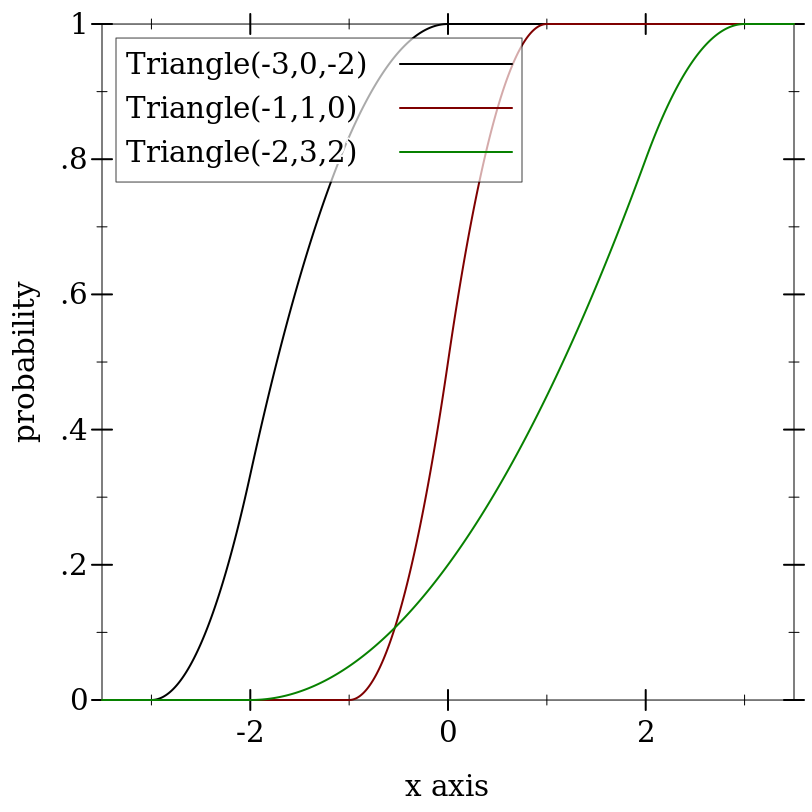
> (plot (for/list ([a (in-list '(-3 -1 -2))] [b (in-list '(0 1 3))] [m (in-list '(-2 0 2))] [i (in-naturals)]) (function (ordered-dist-cdf (triangle-dist a b m)) #:color i #:label (format "Triangle(~a,~a,~a)" a b m))) #:x-min -3.5 #:x-max 3.5 #:y-label "probability")
(triangle-dist c c c) for any real c behaves like a support-limited delta distribution centered at c.
9.5.11 Truncated Distributions
syntax
procedure
(truncated-dist d) → Truncated-Dist
d : Real-Dist (truncated-dist d max) → Truncated-Dist d : Real-Dist max : Real (truncated-dist d min max) → Truncated-Dist d : Real-Dist min : Real max : Real
procedure
t : Truncated-Dist
procedure
(truncated-dist-min t) → Flonum
t : Truncated-Dist
procedure
(truncated-dist-max t) → Flonum
t : Truncated-Dist
(truncated-dist d) is equivalent to (truncated-dist d -inf.0 +inf.0). (truncated-dist d max) is equivalent to (truncated-dist d -inf.0 max). If min > max, they are swapped before constructing the distribution object.
Samples are taken by applying the truncated distribution’s inverse cdf to uniform samples.
> (define d (normal-dist)) > (define t (truncated-dist d -2 1)) > t (truncated-dist (normal-dist 0.0 1.0) -2.0 1.0)
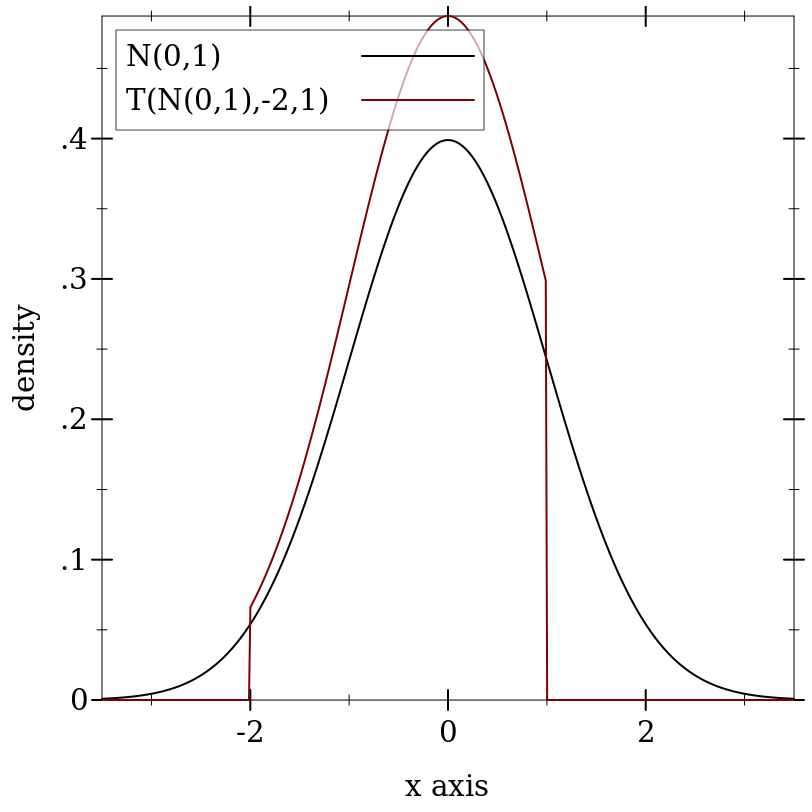
> (plot (list (function (distribution-pdf d) #:label "N(0,1)" #:color 0) (function (distribution-pdf t) #:label "T(N(0,1),-2,1)")) #:x-min -3.5 #:x-max 3.5 #:y-label "density")
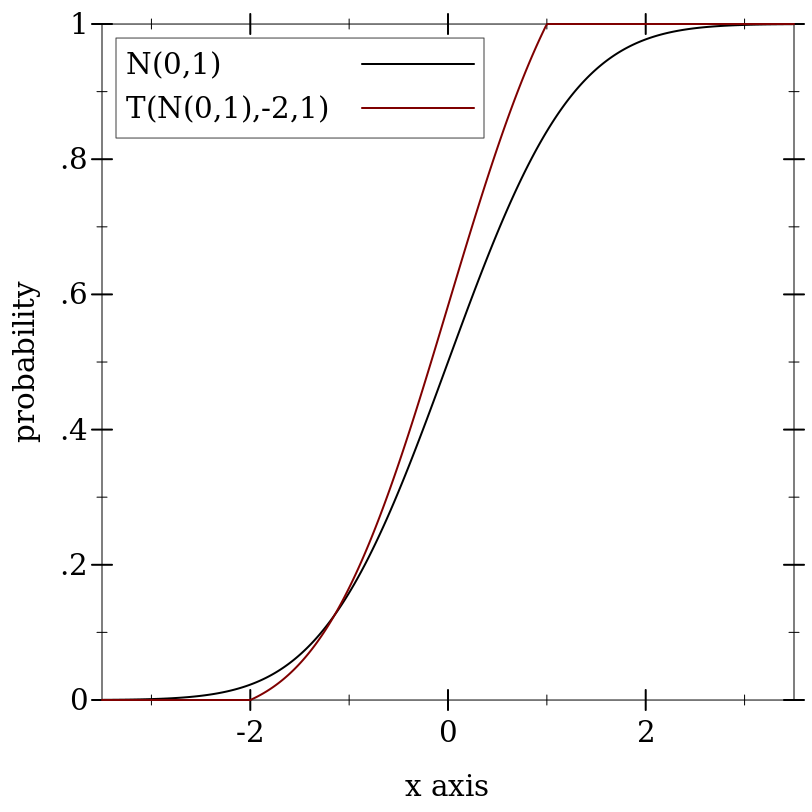
> (plot (list (function (ordered-dist-cdf d) #:label "N(0,1)" #:color 0) (function (ordered-dist-cdf t) #:label "T(N(0,1),-2,1)")) #:x-min -3.5 #:x-max 3.5 #:y-label "probability")
9.5.12 Uniform Distributions
Wikipedia: Uniform Distribution.
syntax
procedure
(uniform-dist max) → Uniform-Dist max : Real (uniform-dist min max) → Uniform-Dist min : Real max : Real
procedure
(uniform-dist-min d) → Flonum
d : Uniform-Dist
procedure
(uniform-dist-max d) → Flonum
d : Uniform-Dist
(uniform-dist) is equivalent to (uniform-dist 0 1). (uniform-dist max) is equivalent to (uniform-dist 0 max). If max < min, they are swapped before constructing the distribution object.
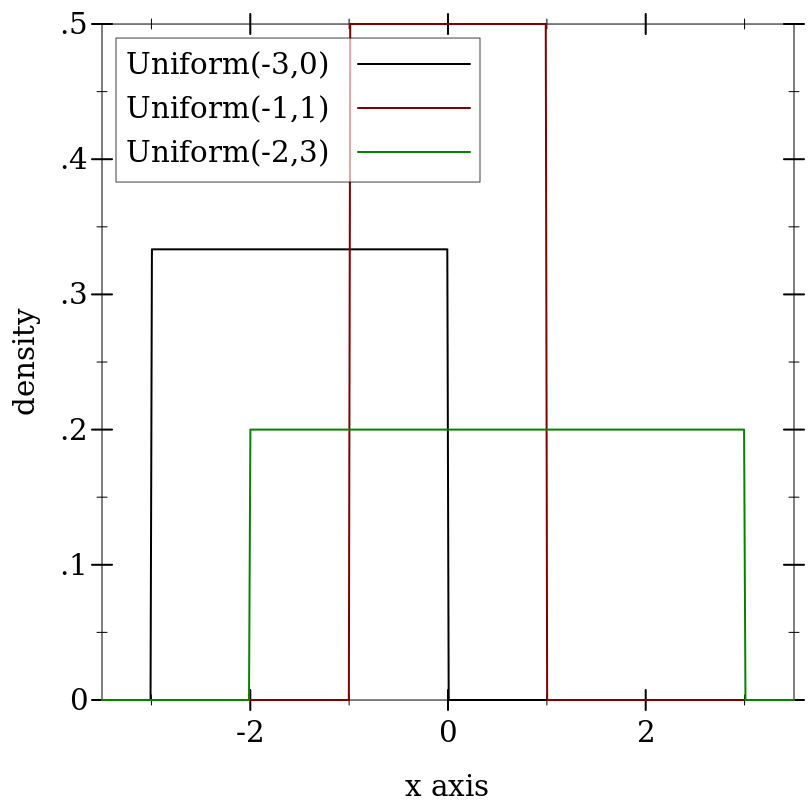
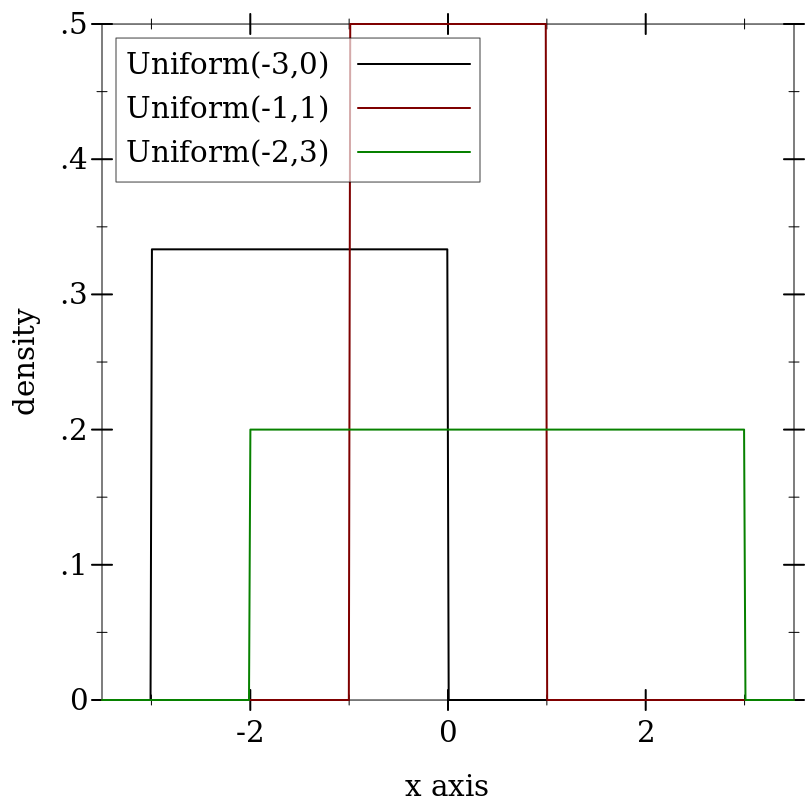
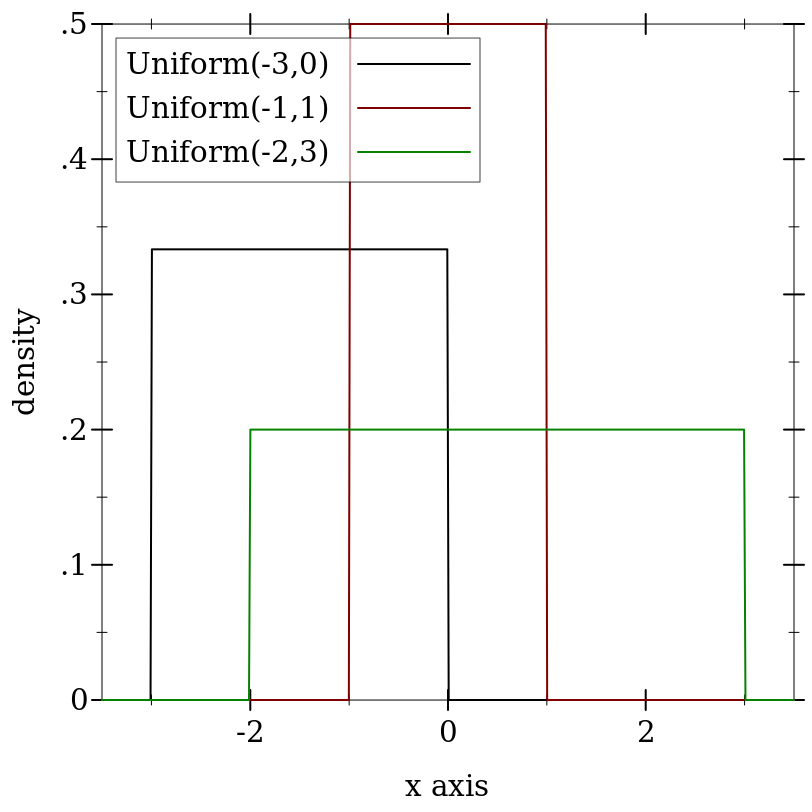
> (plot (for/list ([a (in-list '(-3 -1 -2))] [b (in-list '(0 1 3))] [i (in-naturals)]) (function (distribution-pdf (uniform-dist a b)) #:color i #:label (format "Uniform(~a,~a)" a b))) #:x-min -3.5 #:x-max 3.5 #:y-label "density")
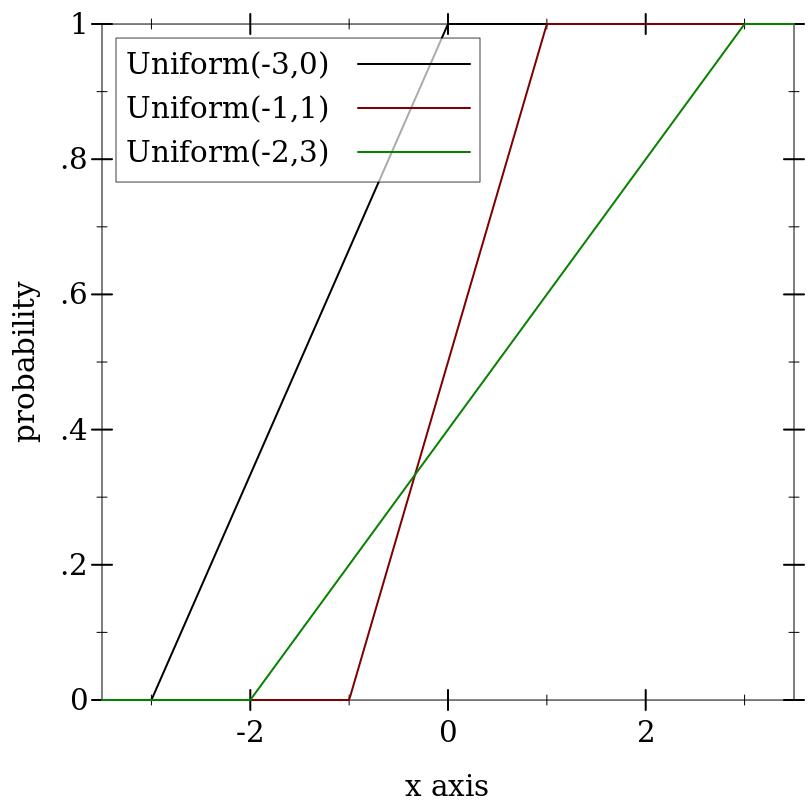
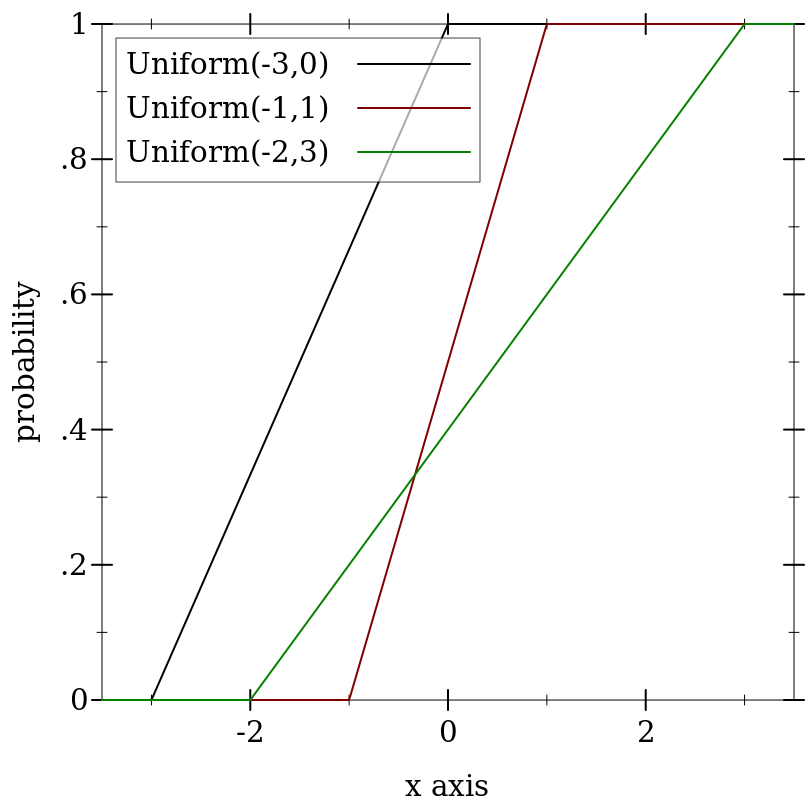
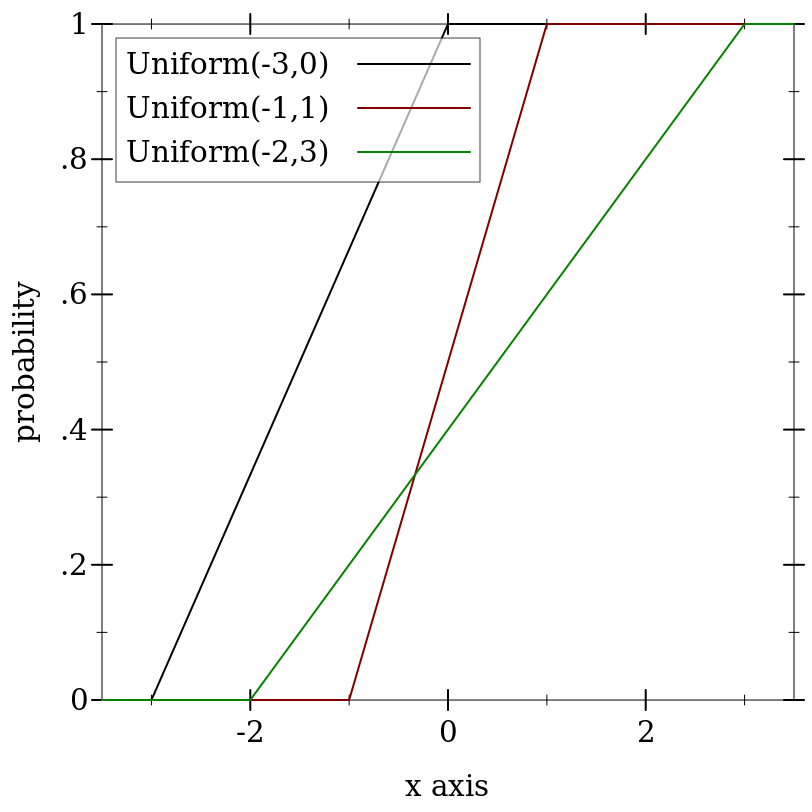
> (plot (for/list ([a (in-list '(-3 -1 -2))] [b (in-list '(0 1 3))] [i (in-naturals)]) (function (ordered-dist-cdf (uniform-dist a b)) #:color i #:label (format "Uniform(~a,~a)" a b))) #:x-min -3.5 #:x-max 3.5 #:y-label "probability")
(uniform-dist x x) for any real x behaves like a support-limited delta distribution centered at x.