Department of Computer Science
Rice University
Houston, Texas 77005-1892
Robert Bruce Findler Matthew Flatt
Department of Computer Science
![]()
Rice University
Houston, Texas 77005-1892
DRAFT: July 18, 1998
Module and class systems have evolved to meet the demand for reuseable software components. Considerable effort has been invested in developing new module and class systems, and in demonstrating how each promotes code reuse. However, relatively little has been said about the interaction of these constructs, and how using modules and classes together can improve programs. In this paper, we demonstrate the synergy of a particular form of modules and classes--called units and mixins, respectively--for solving complex reuse problems in a natural manner.
Module and class systems both promote code reuse. In theory, many uses of classes can be simulated with modules, and vice versa. Experience shows, however, that programmers need both constructs because they serve different purposes [43]. A module delineates boundaries for separate development. A class permits fine-grained reuse via selective inheritance and overriding.
Since modules and classes aid different patterns of reuse, modern languages provide separate constructs for each. Unfortunately, the reuse allowed by conventional module and class systems is limited. In these systems, modules and classes are hard-wired to a specific context, i.e., to specific modules or to a specific superclass.
In previous work, we separately described the novel module and class systems in MzScheme [12]. MzScheme's modules [13], called units, are roughly like Java packages, except that units are linked through an external linking specification, instead of through a fixed internal specification. MzScheme's object language [14] provides mixins, which are like Java classes except that a mixin is parameterized over its superclass, so it can be applied multiple times to create different derived classes from different base classes. The advantages of units and mixins over conventional module and class languages follow from a single language design principle: specify connections between modules or classes separately from their definitions.
The shared principle of separating connections from definitions makes units and mixins synergistic. When units and mixins are combined, a programmer can exploit the encapsulation and linking properties of units to control the application of mixin extensions (e.g., to change the class extended by a particular mixin).
In Section 5, we motivate in more detail the design behind MzScheme's units and mixins, but their synergy is best demonstrated with an example. The bulk of this paper therefore presents an in-depth example, showing how the synergy of units and mixins solves an old extensibility problem [7, 40] in a natural manner. Section 2 describes the extensibility problem, and Section 3 develops a rough solution the problem using conventional classes. Section 4 introduces units and mixins to refine and complete the solution. Sections 5 and 6 extract lessons from the example for the design of modular object-oriented programming languages. Finally, Section 7 relates our work to other research.
The following table summarizes the extensibility problem:
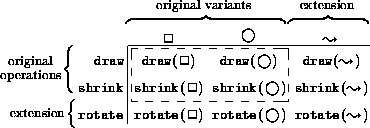
The portion of the table contained in the dotted box represents a program component that provides several operations, draw and shrink, on a collection of data, geometric shapes like squares and circles. A programmer may wish to use such a component in three different contexts:
Neither standard functional nor object-oriented strategies offer a satisfactory way to implement the component and its clients. In a functional language, the variants can be implemented as a type, with the operations as functions on the type. Using this approach, the set of operations is easily extended, but adding a new variant requires modifying the functions. In an object-oriented language, the variants can be implemented as a collection of classes, with the operations as methods common to all of the classes. Using this approach, the datatype is easily extended with a new variant, but adding a new operation is typically implemented by modifying the classes.
The existing literature provides three solutions to the problem. Kühne's [24] solution, which relies on generic procedures with double-dispatching, can interfere with the hierarchical structure of the program. Palsberg and Jay's [32] solution is based on reflection operators and incurs a substantial run-time penalty. Krishnamurthi, Felleisen, and Friedman [11, 23] propose an efficient solution that works with standard class mechanisms, but it requires the implementation (and maintenance) of a complex programming protocol. All of these solutions are partial because they do not address the reuse of clients. In contrast, the combination of units and mixins solves the problem simply and elegantly, and it addresses the reuse of both the original component and its clients.
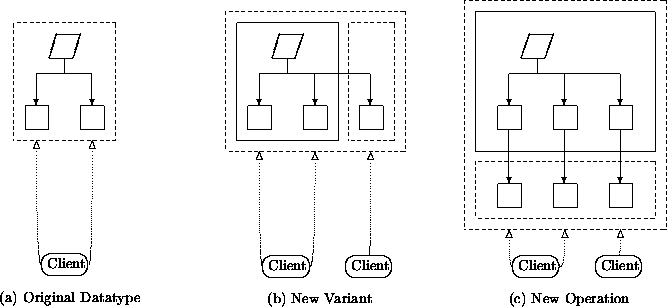
Figure 1: Extensible programming on datatypes
Figure 1 outlines our solution to the extensibility problem:
Shape Datatype |
|
|
Initially, our shape datatype consists of three variants and one
operation: rectangles, circles, and translated shapes for drawing.
The rectangle and circle variants contain numbers that describe the
dimensions of the shape. The translated variant consists of two
numbers, The shape datatype is defined by the Shape interface and implemented by three classes: Rectangle, Circle and Translated. Each subclass declares a draw method, which is required to implement the Shape interface. Figure 2 shows the interface and class definitions using MzScheme's class system. (MzScheme's class system is similar to Java's; for details, see the Appendix.)
|
(define Shape(interface()draw))Complete Program Figure 2: Shape classes
|
|
Figure 3 contains clients for the shape datatype. The function display-shape consumes a shape and draws it in a new window. The final expression creates a shape and displays it. As the shape datatype is extended, we consider how these clients are affected. |
(define display-shape
(lambda(shape)
(if(not(is-a?shapeShape))
(error``expectedaShape''))
(let([window
Complete Program
Figure 3: Two shape clients
|
Variant Extension |
|
|
To create more interesting configurations of shapes, we extend the shape
datatype with a new variant representing the union of two shapes. Following
the strategy suggested in Figure 1 (b), we define a
new Union class derived from
Shape. Figure 4 defines the
Union class, and shows an expression that uses the new class.
The simplicity of the variant extension reflects the natural expressiveness of object-oriented programming. The object-oriented approach also lets us add this variant without modifying the original code or the existing clients in Figure 3.
|
(define Union
(class*null(Shape)(leftright)
(public
[draw(lambda(windowxy)
(sendleftdrawwindowxy)
(sendrightdrawwindowxy))])))
Complete Program
Figure 4: Variant extension and a new client
|
Operation Extension |
|
|
Shapes look better when they are drawn centered in their windows. We
can support centered shapes by adding the operation
bounding-box, which computes the smallest rectangle
enclosing a shape.
We add an operation to our shape datatype by defining four new classes, each derived from the variants of Shape in Section 3.2. Figure 5 defines the extended classes BB-Circle, BB-Rectangle, BB-Translated, and BB-Union, each providing the bounding-box method. It also defines the BB-Shape interface, which describes the extended shape type for the bounding box classes just as Shape describes the type for the original shape classes. The new display-shape client in Figure 5 uses bounding box information to center its shape in a window. Unfortunately, we must also modify the clients so they create instances of the new bounding box classes instead of the original shape classes, including clients that do not use bounding box information. Thus, the standard object-oriented architecture does not satisfy our original goal; it does not support operation extensions to the shape datatype without modifying existing clients. Since object-oriented programming constructs do not address this problem directly, we must resort to a programming protocol or pattern. In this case, the Abstract Factory pattern [15] and a mutable reference solves the problem. The Abstract Factory pattern relies on one object, called the factory, to create instances of the shape classes. The factory supplies one creation method for each variant of the shape, and clients create shapes by calling these methods instead of using make-object directly. To change the classes that are instantiated by clients, it is only necessary to change the factory, which is stored in the mutable reference. A revised client, using the Abstract Factory, is shown in Figure 6.
The Abstract Factory pattern implements a simple dynamic linker, where
set! installs the link. |
(define BB-Shape(interface(Shape)bounding-box))Complete Program Figure 5: Operation extension
(set!factoryComplete Program Figure 6: Revised clients using Abstract Factory
|
Better Reuse through Units and Mixins |
|
|
In the previous section, we developed the Shape datatype and
its collection of operations, and we showed how object-oriented
programming supports new variants and operations in separately
developed extensions. In this section, we make the separate
development explicit using MzScheme's module system; the basic
definitions, the extensions, and the clients are all defined in
separate modules. MzScheme supports separate compilation for these
modules, and provides a flexible language for linking them. Indeed,
the linking implemented with an Abstract Factory in the previous
section can be more naturally defined through module
linking. Finally, we show how MzScheme's class-module combination
provides new opportunities for reuse that are not available in
conventional object-oriented languages.
|
|
Unitizing the Basic Shapes |
|
|
A module in MzScheme is called a
unit. Figure 7 shows the basic
shape classes encapsulated in a BASIC-SHAPES unit. This unit
imports nothing and exports all of the basic shape classes. The body
of the unit contains the class definitions exactly as they appear in
Figure 2.
In general, the shape of a unit expression is (unit(importvariable (centered ellipses indicate repeated syntactic patterns). The unit-body-exprs have the same form as top-level Scheme expressions, allowing a mixture of expressions and definitions, but define within a unit expression creates a unit-local variable instead of a top-level variable. The unit's imported variables are bound within the unit-body-exprs. Each exported variable must be defined by some unit-body-expr. Unexported variables that are defined in the unit-body-exprs are private to the unit. Figure 8 defines two client units of BASIC-SHAPES: GUI and PICTURE. The GUI unit provides the function display-shape (the same as in Figure 3). Since it only depends on the functionality in the Shape type, not the specific variants, it only imports Shape. The PICTURE unit imports all of the shape variants--so it can construct instances--as well as the display-shape function, and it exports nothing. When PICTURE is invoked as part of a program, it constructs a shape and displays it. A unit is an unevaluated bundle of code, much like a ``.o'' object file created by compiling a traditional language. At the point where BASIC-SHAPES, GUI, and PICTURE are defined as units, no shape classes have been defined, no instances have been created, and no drawing window has been opened. Each unit encapsulates its definitions and expressions without evaluating them until the unit is invoked, just like a procedure encapsulates expressions until it is applied. However, none of the units in Figures 7 and 8 can be invoked directly because each unit requires imports. The units must first be linked together to form a program.
|
(define BASIC-SHAPES
(unit(import)
(exportShapeRectangleCircleTranslated)
(define Shape(interface
Complete Program
Figure 7: Creating Units
(define GUI
(unit(importShape)
(exportdisplay-shape)
(define display-shape
Complete Program
Figure 8: Unitized shape clients
|
Linking the Shape and Client Units |
|
|
Units are linked together with the compound-unit form.
Figure 9 shows how to link the units of the
previous sub-section into a complete program:
BASIC-PROGRAM. The PICTURE unit's imports are not
a priori associated with the classes in BASIC-SHAPES.
This association is established only by the compound-unit
expression, and it is established only in the context of
BASIC-PROGRAM. The PICTURE unit can be reused with
different Shape classes in other compound units.
The compound-unit form links several units, called constituent units, into one new compound unit. The linking process matches imported variables in each constituent unit with either variables exported by other constituents, or variables imported into the compound unit. The compound unit can then re-export some of the variables exported by the constituents. Thus, BASIC-PROGRAM is a unit with imports and exports, just like BASIC-SHAPES or GUI, and no evaluation of the unit bodies has occurred. But, unlike the BASIC-SHAPES and GUI units, BASIC-PROGRAM is a complete program because it has no imports. Each compound-unit expression (compound-unit(importvariable has three parts:
To evaluate a compound-unit expression, the exprs in
the link clause are evaluated to determine the compound
unit's constituents. For each constituent, the number of variables it
imports must match the number of linkspecs provided;
otherwise, an exception is raised. Each linkspec is matched
to an imported variable by position.
Once a compound unit's constituents are linked, the compound unit is
indistinguishable from an atomic unit. Conceptually, linking creates
a new unit by merging the internal expressions and definitions from
all the constituent units. During this merge, variables are renamed as
necessary to implement linking between constituents and to avoid name
collisions between unrelated variables. The merged
unit-body-exprs are ordered to match the order of the
constituents in the compound-unit's link
clause.
|
(define BASIC-PROGRAM
(compound-unit
(import)
(link[S(BASIC-SHAPES)]
[G(GUI(SShape))]
[P(PICTURE(SRectangle)(SCircle)(STranslated)
(Gdisplay-shape))])
(export)))
Complete Program
Figure 9: Linking basic shape program
|
Invoking Unit Programs |
|
The BASIC-PROGRAM unit from
Figure 9 is a complete program,
analogous to a conventional application, but the program still has
not been executed. In most languages with module systems, a complete
program is executed through commands outside the language. In
MzScheme, a program unit is executed directly with the
invoke-unit form:
(invoke-unitexpr) The value of expr must be a unit. Invocation evaluates the unit's definitions and expressions, and the result of the last expression in the unit is the result of the invoke-unit expression. Hence, to run BASIC-PROGRAM, evaluate (invoke-unitBASIC-PROGRAM)
|
|
New Units for a New Variant |
|
|
To extend Shape with a Union variant, we define the
extension in its own unit, UNION-SHAPE, as shown in
Figure 10. The Shape class is
imported into UNION-SHAPE, and the new Union class
is exported. In terms of Figure 1 (b),
UNION-SHAPE corresponds to the smaller dashed box, drawn
around the new variant class. The solid box is the
original unmodified BASIC-SHAPES unit, and the outer dashed box in (b)
is BASIC+UNION-SHAPES, a compound unit linking
UNION-SHAPE together with BASIC-SHAPES.
Since the BASIC+UNION-SHAPES unit exports the variants defined by both BASIC-SHAPES and UNION-SHAPE, it can serve as a replacement for the original BASIC-SHAPES unit, yet it can also provide more functionality for new clients. The UNION-PROGRAM unit in Figure 11 demonstrates both of these uses. In this new program, the GUI and PICTURE clients are reused intact from the original program, but they are now linked to BASIC+UNION-SHAPES instead of BASIC-SHAPES. An additional client unit, UNION-PICTURE, takes advantage of the shape extension to draw a superimposed rectangle and circle picture.
|
(define UNION-SHAPE
(unit(importShape)
(exportUnion)
(define Union(class*null(Shape)
Complete Program
Figure 10: Variant extension in a unit
(define UNION-PICTURE
(unit(importRectangleCircleTranslatedUnion
display-shape)
(export)
(display-shape(make-object
Complete Program
Figure 11: New client and the extended program
|
New Units and Mixins for a New Operation |
|
|
To extend Shape with a bounding-box operation, we
define the BB-SHAPES unit in
Figure 12. This unit corresponds to the
smaller dashed box in Figure 1 (c).
The BB-SHAPES unit is the first example to rely on mixins. The BB-Rectangle class is derived from an imported Rectangle class, which is not determined until the unit is linked--long after the unit is compiled. Thus, BB-Rectangle defines a mixin, a class extension that is parameterized over its superclass.
The compound unit BASIC+UNION+BB-SHAPES links the
BASIC+UNION-SHAPES unit from the previous section with the
new bounding-box unit, then exports the bounding-box classes. As the
bounding-box classes are exported, they are renamed to match the
original class names, As before, the BASIC+UNION+BB-SHAPES unit serves as a replacement for either BASIC-SHAPES or BASIC+UNION-SHAPES, and also provides new functionality for new clients. One new client is BB-GUI (see Figure 13), which provides a display-shape that exploits bounding box information to center a shape in a window. The BB-GUI unit replaces GUI, but we reuse PICTURE and UNION-PICTURE without modifying them. An Abstract Factory is unnecessary because units already permit us to vary the connection between the shape-creating clients and the instantiated classes. Putting everything together produces the new program BB-PROGRAM at the bottom of Figure 13.
|
(define BB-SHAPES
(unit(importShapeRectangleCircleTranslatedUnion)
(exportBB-ShapeBB-RectangleBB-Circle
BB-TranslatedBB-UnionBB)
(define BB-Shape(interface(Shape)
Complete Program
Figure 12: Operation extension in a unit
(define BB-GUI
(unit(importBB-ShapeBB)
(exportdisplay-shape)
(define display-shape
(lambda(shape)
(if(not(is-a?shapeBB-Shape))
Complete Program
Figure 13: Program with the operation extension
|
Synergy at Work |
|
|
The shape example demonstrates the synergy of units and mixins.
Units, by separating the definition and linking of modules, support
the reuse of PICTURE and UNION-PICTURE as the shape
representation evolves. Mixins, by abstracting a class expression over an
imported class, enable the encapsulation of each extension in its own
unit. The combination of units and mixins thus enables a direct
translation of the ideal program structure from
Figure 1 into a working program.
We have achieved the complete reuse of existing code at every stage in the extension of Shape, but even more reuse is possible. The code in Figure 14 illustrates how units and mixins combine to allow the use of one extension multiple times. The COLOR-SHAPE unit imports a Shape class and extends it to handle colors. With this single unit containing a single mixin, we can extend all four of the shape variants: Rectangle, Circle, Translated, and Union. The compound unit BASIC+UNION+BB+COLOR-SHAPES in Figure 14 uses the COLOR-SHAPE unit four times to obtain the set of color shape classes. The code in Figure 14 uses a few features that are not described in this paper (the rename clause in a class* expression, and the use of args to stand for multiple arguments, passed on to super-init with apply). These details are covered in the MzScheme reference manual [12]. The point here is that units and mixins open new avenues for reuse on a large scale.
|
(define COLOR-SHAPE
(unit(importShape)
(exportC-Shape)
(define C-Shape
(class*Shape()args
(rename
[super-drawdraw])
(public
[color``black'']
[change-color
(lambda(c)
(set!colorc))]
[draw
(lambda(windowxy)
(sendwindowset-colorcolor)
(super-drawwindowxy))])
(sequence
(applysuper-initargs))))))
Complete Program
Figure 14: Reusing a class extension
|
A module system serves two key purposes:
To serve their distinct purposes, modules and classes require distinct constructs in a programming language, but these constructs interact. In our example program, the collection of geometric shapes is naturally implemented as a set of Shape classes. The implementation of the shape classes and the client code that uses them are defined in separate modules. Using classes to represent shapes makes it easy to extend the shape classes without modifying the basic definition of a shape. Separating the definition of shapes from their use in different modules makes it easy to replace the original shape classes with new classes without modifying the client. This is precisely how modular object-oriented code is supposed to work.
Unfortunately, the existing module-class combinations do not support this sort of modular object-oriented programming. In Java, for example, if the Rectangle class is extended, then a client module that creates Rectangle instances must be modified to refer to the new, extended class. The root of this problem, both in Java and many other object-oriented languages, is that the connections between modules are hard-wired within the modules. For example, client modules declare that they import the shape module instead of importing a shape module.
The design of module and class constructs must encourage the interaction of the constructs. The Shape example suggests a lesson for the design of modules:
Separate a module's linking specification from its encapsulated definitions.In other words, a module should describe its imports with enough detail to support separate compilation, but the module should not specify the source of its imports. Instead, the imports should be supplied externally by a linking expression.
A module system with external linking in turn constrains the design of the class system. A module may encapsulate a class definition with an imported superclass (e.g., BB-Rectangle in Figure 12). Since module linking is specified outside the module, the superclass is not determined until the module is linked, so the class expression is de facto parameterized over its superclass. Such a parameterized class is a mixin. Mixins tend to be computationally more expensive than classes, but the cost is small [14]. In parallel to the lesson for modules, the requirement to support mixins can be stated as follows:
Separate a class's superclass specification from its extending definitions.Mixins are valuable in their own right. While classes enable reuse because each class can be extended and refined by defining new subclasses, the reuse is one-sided: each class can be extended in many different ways, but each extension applies only to its superclass. A mixin is parameterized with respect to its superclass, so it can add functionality to many different classes. Thus, the reuse potential of a mixin is greater than that of a class.
Others have explored a similar combination of classes and modules in a typed setting. The module systems in Objective Caml [28, 38] and OML [39] support externally specified connections, and since a class can be defined within a module, these languages also provide a form of mixins. However, the modules and mixins in these languages fail to support the synergy we have demonstrated for units and mixins. In particular, they do not allow the operation extension demonstrated in Section 4 because an imported class must match the expected type exactly--no extra methods are allowed. In our example, PICTURE is initially linked to the Rectangle class and later linked to BB-Rectangle; since the latter has more methods, neither Objective Caml nor OML would allow PICTURE to be reused in this way. Our example thus suggests a third lesson for the design of module and class type systems:
Allow subsumption for connections, including both module linking and class extension.
Much of the previous research on modules and classes focused on unifying the constructs. Lee and Friedman [26, 27] investigated languages that work directly on variables and bindings, which provides a theoretical foundation for implementing both modules and classes. Similarly, Jagannathan [21] and Miller and Rozas [29] proposed first-class environments as a common mechanism. Bracha [3] has explored mixins for both modular and object-oriented programming; Ancona and Zucca [1] provide a categorical treatment of this view. Our work is complementary to all of the above work, because we focus on designing the constructs to be used by a programmer, rather than the method used to implement those constructs.
Languages that have promoted modularization, including Mesa [31], Modula-2 [45], and SML [30], provide no direct support for object-oriented programming. Similarly, early object-oriented languages, such as Simula 67 [9] and Smalltalk [16], provide no module system. In contrast, languages such as Ada 95 [20], Common Lisp [42], Dylan [41], Haskell [19], Java [17], and Modula-3 [18] provide both modules and classes. For Cecil [4], Chambers and Leavens [5] designed a module system specifically to complement a class system with multi-methods. Unfortunately, these module and class systems do not support external connections--a central principle of our design that is crucial to software engineering (see Section 5).
Scheme [6] provides no specific mechanisms for modular or
object-oriented programming. Instead, Scheme supports modular
programming through lexical scope, and many implementations provide
separate compilation for top-level expressions. Programmers can
regard top-level expressions as ``modules'' that hide private
definitions by using let or letrec. A number of
Scheme systems have been developed that codify the
module-via-top-level
idea [8, 10, 36, 35, 44], but
none of these satisfies the criteria in
Section 5. In contrast, Kelsey's proposed module
system [22] captures many of the same ideas as
units. Scheme can also support object-oriented programming by
simulating objects with procedures and classes with higher-order
procedures [37]. Several object-oriented
extensions for Scheme have been developed [2, 34],
including some that support
mixins [25, 33].![]() However, none of these systems provide complete
languages for both modular and object-oriented programming.
However, none of these systems provide complete
languages for both modular and object-oriented programming.
Units and mixins promote a synergistic integration of modular and object-oriented programming techniques. The combination succeeds due to a consistent separation of definitions (encapsulated in modules or classes) from connections (between modules or classes) in both units and mixins.
The bulk of the paper explores the extensibility problem because it highlights many of the advantages of units and mixins. Strictly speaking, the problem can be solved using conventional module and class systems and the Abstract Factory pattern. Nevertheless, a straightforward datatype implementation using units and mixins is more immediately extensible. This natural bias towards reuse and extension is the essential benefit of units and mixins.
For a complete version of the code presented here, see
http://www.cs.utah.edu/plt/publications/icfp98-ff/
The authors would like to thank Matthias Felleisen, Corky Cartwright, John Clements, Dan Friedman, Shriram Krishnamurthi, Paul Steckler, and the anonymous reviewers.
The shape of a MzScheme class declaration is:
(class* superclass-expr(interface-expr)(init-variable
) instance-variable-clause
)
(centered ellipses indicate repeated patterns). The expression superclass-expr determines the superclass for the new class, and the interface-exprs specify the interfaces implemented by the class. The init-variables receive instance-specific initialization values when the class is instantiated (like the arguments supplied with new in Java). Finally, the instance-variable-clauses define the instance variables of the class, plus expressions to be evaluated for each instance. For example, a public clause declares public instance variables and methods.
Thus, the definition
(define Rectangle
(class*null(Shape)(widthheight)
(public
[draw(lambda(windowxy)  )])))
)])))
introduces the base class Rectangle. The null indicates that Rectangle is not derived from any class, (Shape) indicates that it implements the Shape interface, and (width height) indicates that two initialization arguments are consumed for initializing an instance. There is one instance-variable-clause that defines a public method: draw.
MzScheme's object system does not distinguish between instance
variables and methods. Instead, procedure-valued instance variables
act like methods. The draw declaration in Rectangle
defines an instance variable, and (lambda (window x y) ![]() )
is its initial value expression, evaluated once per instance. When
draw is called as the method of some object, draw
may refer to the object via this. In most object-oriented
languages, this is passed in as an implicit argument to a
method; in MzScheme, this is part of the environment for
evaluating initialization expression, so each ``method'' in an object
is a closure containing the correct value of
this.
)
is its initial value expression, evaluated once per instance. When
draw is called as the method of some object, draw
may refer to the object via this. In most object-oriented
languages, this is passed in as an implicit argument to a
method; in MzScheme, this is part of the environment for
evaluating initialization expression, so each ``method'' in an object
is a closure containing the correct value of
this.![]()
An instance of Rectangle is created using the make-object primitive. Along with the class to instantiate, make-object takes any initialization arguments that are expected for the class. In the case of Rectangle, two initialization arguments specify the size of the shape:
(define rect(make-objectRectangle50100))
The value of an instance variable is extracted from an object using ivar. The following expression calls the draw ``method'' of rect by extracting the value of draw and applying it as a procedure:
((ivarrectdraw)window00)
Since method calls of this form are common, MzScheme provides a send macro. The following send expression is equivalent to the above ivar expression:
(sendrectdrawwindow00)
An interface is declared in MzScheme using the interface form:
(interface(superinterface-expr) variable
)
The superinterface-exprs specify all of the superinterfaces for the new interface, and the variables are the instance variables required by the interface (in addition to variables declared by the superinterfaces). For example, the definition
(define Shape(interface()draw))
creates an interface named Shape with one variable: draw. Every class that implements Shape must declare a draw instance variable. The definition
(define BB-Shape(interface(Shape)bounding-box))
creates an interface named BB-Shape with two variables: draw and bounding-box. Since Shape is the superinterface of BB-Shape, every class that implements BB-Shape also implements Shape.
A class implements an interface only when it specifically declares the implementation (as in Java). Thus, the Rectangle class in the previous section only implements the Shape interface.
The definition
(define BB-Rectangle
(class*Rectangle(BB-Shape)(widthheight)
(public[bounding-box  ])
(sequence(super-initwidthheight))))
])
(sequence(super-initwidthheight))))
derives a BB-Rectangle class that implements BB-Shape. The draw method, required to implement BB-Shape, is inherited from Rectangle.
The BB-Rectangle class declares the new bounding-box method. It also includes a sequence clause that calls super-init. A sequence clause declares expressions to be evaluated for each instance. It is commonly used to call the special super-init procedure, which initializes the part of the instance defined by the superclass (like calling super in a Java constructor); a derived class must call super-init exactly once for every instance. In the case of BB-Rectangle, calling super-init performs Rectangle's initialization for the instance. BB-Rectangle provides two arguments to super-init because the Rectangle class consumes two initialization arguments.
Modular Object-Oriented Programming with Units and Mixins
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds, with bug fixes and extensions by Matthew.
The command line arguments were:
latex2html -split 0 u+m.sub.tex.
The translation was initiated by on Sat Jul 18 14:02:42 DST 1998